小池有话说

我假设你已经知道了什么是图灵机。

事实上， 图灵机不能算出所有的 可计算数，它只能算出0和1之间的可计算数。因为0和1之间的实数和所有的实数一样多, 所以, 图灵机也就可以计算出所有的可计算数了. 图灵机只能计算出0和1之间的数, 是因为图灵机表示数的方式是这样的:

图灵机的纸带是向右无限延伸的，它用二进制表示实数，小数点在看不见的最左面。

如果图灵机的纸带上是这样的数$1,0,0,0,\cdots$, 从左往右数, 第一个数字1表示1/2, 第二个数字0的权是1/4,第三个数字0的权是1/8, 如此等等. 那么这个数整体就表示二进制的1/2, 即0.5.

接下来我们看看 图灵机如何计算1/2:

很简单, 初始处于begin状态, 打印一个1, 然后转到print0状态不断打印0就可以了. L和R表示左或者右, P表示打印, 后面跟着的字母表示要打印的东西.

这个图灵机在这里, 你可以亲手操作一个虚拟的图灵机.

然后我们看看 图灵机如何计算1

这个也很简单, 就是一个不断打印1的过程.

接下来一个有点复杂, 是一个 打印1/3 的过程. 1/3在二进制中的表示是这样的 $0.01010101\cdots$. 如下图所示

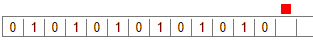
如果你还有疑惑, 请移步1/3在二进制中如何表示?

配置表是这样的

好了, 打印了这么多都是有理数, 图灵机可不可以计算 无理数 呢? 当然可以了.

你或许想计算 $\sqrt 2$, 那对我们来说太困难了, 或许我会单独写一篇博客的, 现在, 我们先计算一个很有意思的数, 这个数是这样的, $0.01011011101111011111\cdots$

换言之, 用0间隔着1, 先是一个1, 再是2个1, 再是3个1, 如此以至无穷.

如果能用伪代码描述, 这个数是这样的:

let i = 0
while true:
    print 0
    repeat i times { print 1 }
    i++

这个数是无理数(有理数在二进制下一定是循环小数).

在计算这个数之前, 我们先看一个规则, 就是由图灵订立的规则, 图灵把下图中白色的格子叫做F格, 把灰色的格子叫做E格, F格一旦打印, 就不可擦除, E格打印之后还可以擦除, 最后F格中的才算输出, 将所有F格的数字集合起来, 就是计算结果. 我们可以将F格看成图灵机的显示器, 将E格看成图灵机的内存.

我们准备在图灵机中这样计算:

假设已经计算好了这个数的一部分, 那么 我们就在纸带最右打印一个0和1, 然后就打印和之前最多的那些1相同个数的1. 但是我们如何知道1的个数呢, 图灵采用了一个巧妙的方法, 他把之前的1的相应的E格(相应的E格指的是一个F格右边的E格)都打印上x, 于是, 只要看到一个x, 就打印一个对应的1就可以了.

全部配置如下:

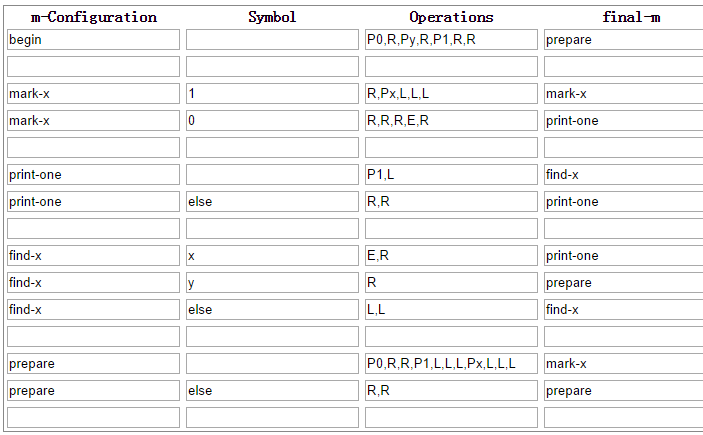
begin 状态就不说了. mark-x 是当指针停在最后的 1 上面时, 开始标记 x.

print-one 是打印n个1的过程, 打印结束后就继续将下一个x转换成1, 所以要先 find-x 以找到x.因为 print-one 状态是从 find-x 状态来的, 此时, find-x 刚刚删除一个x, 因此光标要一直往右走, 这就是 print-one 的else分支做的事情.

find-x用于向左走找到一个x, 找到之后, 擦除x,然后去打印1(print-one). 在向左走找x的过程, find-x不知道什么时候x没有了, 所有, 在begin的过程中, 在最左边的E格打了个y, 以便停止.

prepare 用于打印初始的0和1, 然后转为标记x的过程.

你自己运行之后, 可能会发现, 每次在find-x的过程中, 光标都要移动到最左边, 效率很低. 当然有办法不走那么远的路, 不过意义不大, 图灵机的目的主要是为了研究可计算性, 而不是计算的效率.

二进制加一

我记得有一次google的doodle就是这样的一个图灵机. 我复原出来, 大概是这个样子的.

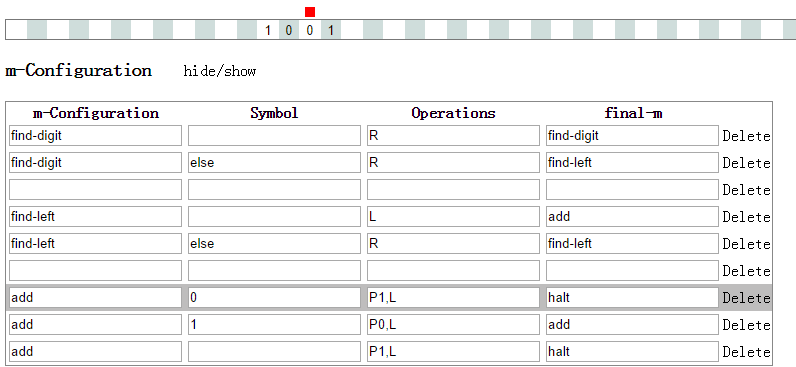
首先, 你需要在某处写个二进制数作为输入. 然后光标会自动前进, 找到数字之后, 开始做加法.

find-digit 用于当光标处在数字左边的时候自动右移.

find-left 用于当光标处在数字上的时候, 找到数字的右边界.

add 用于加一, 当数字是1的时候, 要向左不断加过去(因为有进位), 当数字0的时候, 就加一,然后可以停机了. 如果遇到空格子, 按0处理.

加法

有了加一的程序, 我们可以做加法的程序了.

配置如下:

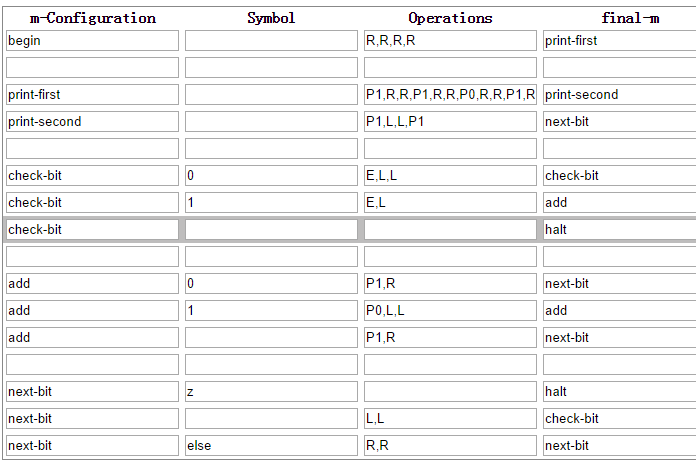
我们的思路是这样的, 我们首先在F格中打印第一个数, 然后再E格中打印第二个数, 右对齐.

begin 跳过几个格子, 为进位留下空间.

print-first 顺序打印第一个数. 我们打印的是1101

print-second 逆序打印第二个数, 我们打印的是11

check-bit 检查第二个数的某一位是0还是1, 如果是0, 就不做什么, 如1, 则开始做加法.

add 加一操作.

next-bit 在第二个位上向右走, 直到遇到最后一位. 然后开始做加法.